背景

话说我们的国产之光大疆创新（DJI）公司不仅很会造无人机，而且还很注重人才的培养。于是，他们就弄出了 RoboMaster 机甲大师系列活动。最开始，它是面向各大高校的机器人比赛。在大疆进军教育市场后，他们的团队又造出了 RoboMaster S1/EP 系列的教育机器人。由于大疆在内部已经做了图形化编程的适配，这类机器人就相对更适合青少年 ~~反正我是玩不惯图形化编程~~，也许有利于扩大市场。

在这样的背景下，大疆联合几所高校（今年为 西安交通大学、电子科技大学、华中科技大学），与其共同开展“疆来计划”，旨在提升青少年，尤其是高中生的科学素养和编程技能。因此我 ~~抱着试试看的态度~~ 本着“能学到东西就是好地方”的宗旨报名参加了今年电子科技大学的“疆来计划”。

当然，要参加是有门槛的，得先做题，还要通过视频面试这样的选拔，才能进入到最终的线上和线下夏令营活动。既然要做题，就肯定少不了一些奇奇怪怪的、平常根本不会想到的思路清奇的题。于是就有了我们这一篇博客。

题目

在“大疆教育平台”下载模拟器，通过“大师之路”的学习，控制EP机器人，在模拟器中完成椭圆形图案的绘制，尽可能用更多的方案绘制出椭圆形轨迹（包括但不限于车头方向不变，车头方向时时改变、车头始终指向焦点等）（提交轨迹绘制截图及程序截图）

那他既然要求用多种方法画椭圆，我就用勉为其难地用给出的三种都做一遍吧。

解法

初始化

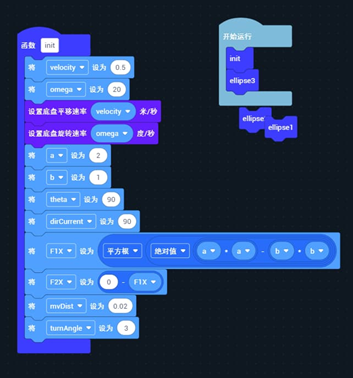
车头方向不变

这种解法参考了 Scratch 画椭圆的方法（百度贴吧）的 9 楼。

效果图示

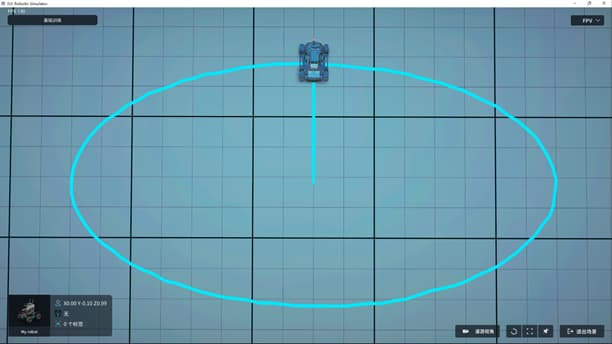
数学原理

椭圆的参数方程：

$$\begin{equation} \left\{ \begin{aligned} x=a\cos\theta\\ y=b\sin\theta\\ \end{aligned} \right. \end{equation}$$

程序实现

代码展示

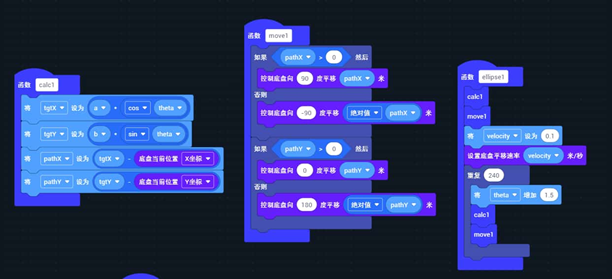
代码解释 (C++)

void ellipse1(){
    calc1();
    move1();
    velocity = 0.1;
    setVelocity(velocity);
    for(int i=0;i<240;i++){
        theta += 1.5;
        calc1();
        move1();
    }
}

// 用椭圆的参数方程计算导航点坐标
void calc1(){
    tgtX = a * cos(theta);
    tgtY = b * sin(theta);
    pathX = tgtX - getX();
    pathY = tgtY - getY();
}

// 移动到导航点
void move1(){
    if(pathX > 0)
        move(90, pathX);
    else
        move(-90, abs(pathX));
    if(pathY > 0)
        move(0, pathY);
    else
        move(180, abs(pathY));
}

车头沿切线

数学原理

椭圆上任意一点 $A$ 到两个焦点 $F_{1}, F_{2}$ 的距离之和 $d$ 始终为一个定值，也就是长轴 $2a$。

那么我们就根据巡线的思路，如果 $d>2a$ 就往里拐，反之就往外拐。

但是，这样会造成小车的路径在椭圆的基准线两侧波动，最后会偏到完全修不回来。

因此，我们引入误差控制，如果 $d>2a$ 那么就往里拐并向里移动 $d-2a$ 米以修正掉由于转向引起的误差。反之，就向外拐并向外移动 $2a-d$ 米。

效果图示

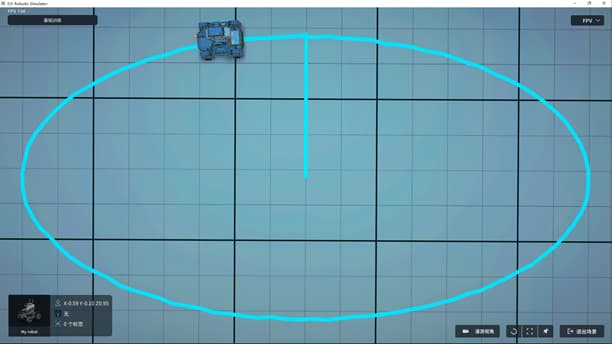
程序实现

代码展示

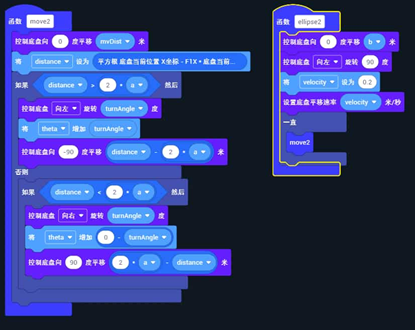
被折叠的代码块是：

将 distance 设置为 $\sqrt{\left( posX - F_{1}X \right)^2 + posY^2} + \sqrt{\left( posX - F_{2}X \right)^2 + posY^2}$。

代码解释 (C++)

void move2(){
    move(0, mvDist);
    distance = sqrt(pow((getX()-F1X), 2) + pow(posY, 2)) + sqrt(pow((getX()-F2X), 2) + pow(posY, 2));
    if(distance > 2*a){
        turn(-1, turnAngle);
        theta += turnAngle;
        move(-90, (distance - 2*a));
    }
    else{
        if(distance < 2*a){
        turn(1, turnAngle);
        theta += turnAngle;
        move(90, (2*a - distance));
        }
    }
}

void ellipse2(){
    move(0, b);
    turn(-1, 90)
    velocity = 0.2;
    setVelocity(velocity);
    while(1)
        move2();
}

车头朝向焦点

数学原理

同上。

但是这里会涉及到车头方向和移动方向的转换。

效果图示

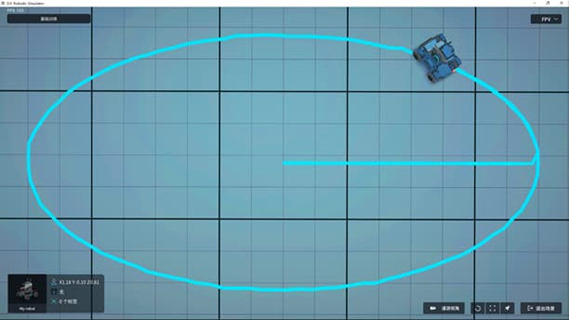
程序实现

代码展示

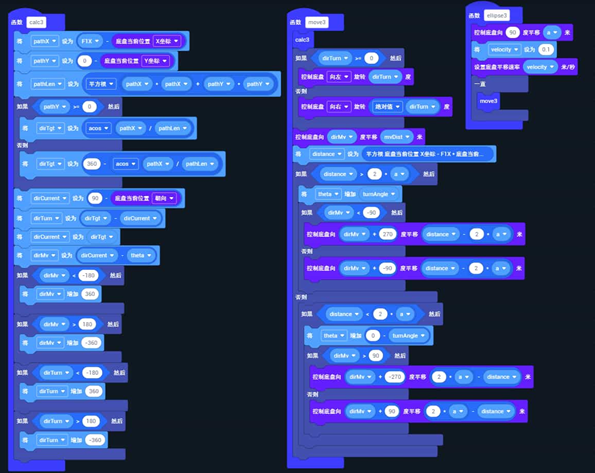
代码解释

void calc3(){
    float pathX = F1X - getX();
    float pathY = 0 - getY();
    float pathLen = sqrt(pow(pathX, 2) + pow(pathY, 2));
    if(pathY >= 0)
        dirTgt = acos(pathX / pathLen);
    else
        dirTgt = 360 - acos(pathX / pathLen);
    dirCurrent = 90 - getDirection();
    dirTurn = dirTgt - dirCurrent;
    dirCurrent = dirTgt;
    dirMv = dirCurrent - theta;
    if(dirMv < -180) dirMv += 360;
    if(dirMv > 180) dirMv -= 360;
    if(dirTurn < -180) dirTurn += 360;
    if(dirTurn > 180) dirTurn -= 360;
}

void move3(){
    calc3();
    if(dirTurn >= 0)
        turn(-1, dirTurn);
    else
        turn(1, abs(dirTurn));
    move(dirMv, mvDist);
    distance = sqrt(pow((getX()-F1X), 2) + pow(posY, 2)) + sqrt(pow((getX()-F2X), 2) + pow(posY, 2));
    if(distance > 2*a){
        theta += turnAngle;
        if(dirMv < -90)
            move((dirMv + 270), (distance - 2*a));
        else
            move((dirMv - 90), (distance - 2*a));
    }
    else{
        theta -= turnAngle;
        if(dirMv > 90)
            move((dirMv - 270), (2*a - distance));
        else
            move((dirMv + 90), (2*a - distance));
    }
}

void ellipse3(){
    move(90, a);
    velocity = 0.1;
    setVelocity(velocity);
    while(1)
        move3();
}