上学期斥巨资购入了一台卡西欧 fx-999CN CW,这个小家伙在实验课上和考试的时候帮了我不少忙。今天我来分享一下如何使用它的数据表格功能和统计功能来加速处理大物实验数据。
要处理的问题
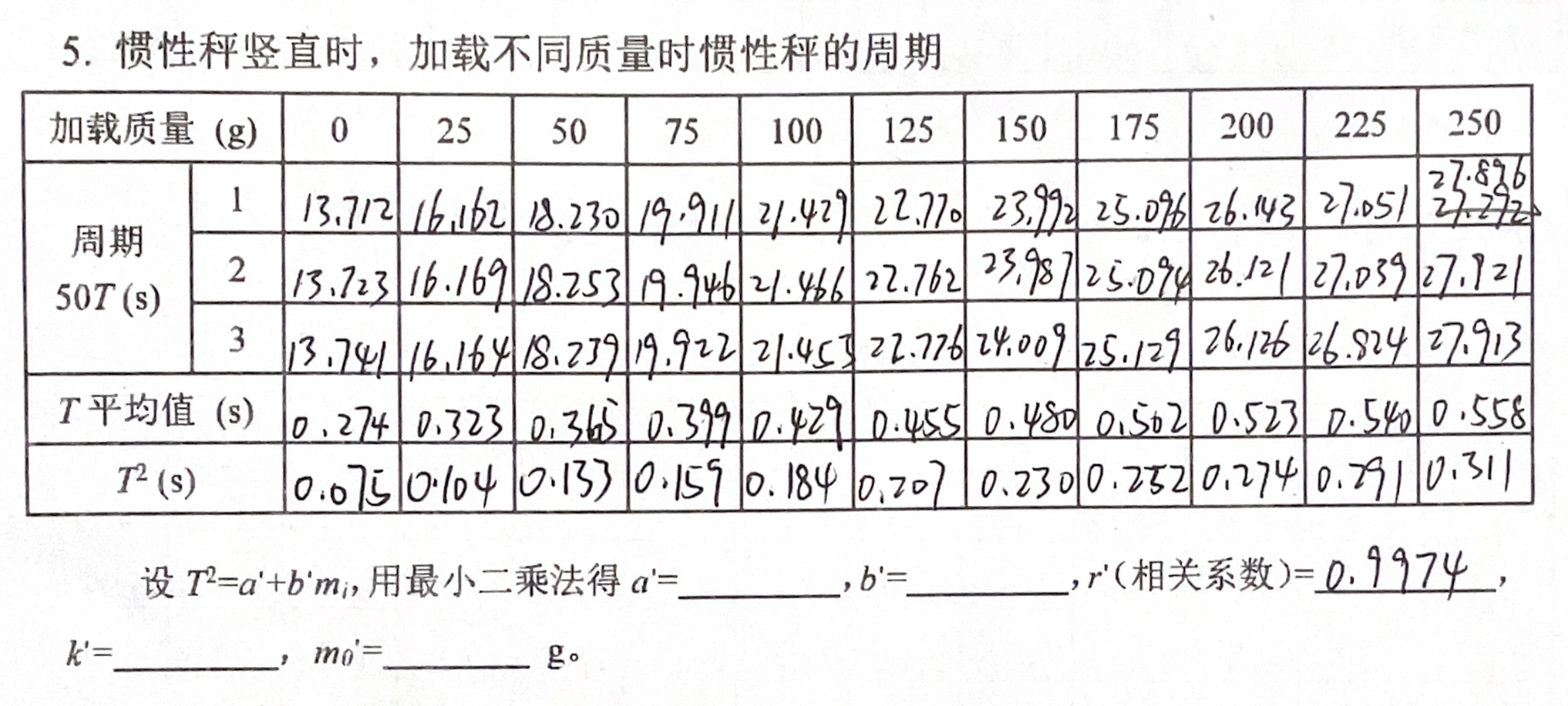
这是我在大物实验课上测得的一组数据,其中第一行 $m$ 是加载质量,$T$ 是振动的周期。我们需要先对三次测得的 $50T$ 数据求平均值,计算出 $\bar{T}$ 和 $T^2$,然后再对 $m$ 和 $T^2$ 的关系进行线性回归。借助计算器,我们可以很快完成这些工作。
利用数据表格功能求 $\bar{T}$ 和 $T^2$
首先,我们将测得的数据输入到数据表格中。打开计算器,按下 主屏幕 键,利用上下左右键选择 数据表格,按下 OK 或这 EXE 进入数据表格编辑界面。

由于 fx-999CN CW 的数据表格只能接受 5 列 x 45 行的数据,我们考虑把实验数据转置一下,并暂时不将 $m$ 的数据输入到表格中。现在,光标高亮在 A1 上,我们键入第一个数据 13.712,然后按下 EXE,光标自动跳到 A2 上,我们继续输入第二个数据 16.162,以此类推。这一组数据录入完成后,我们按下 → 键,光标现在应该跳到 B12 上。然后按几下 ⏫️ 键(位于最右侧,是一个小长条)快速回到 B1,然后录入第二组数据。同理,把第三组数据也录入到表格中。
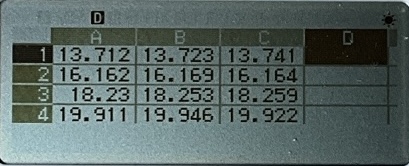
现在,光标来到 D1。我们要在这一列计算出每一个质量 $m$ 对应的 $\bar{T}$。你一定已经会使用 Microsoft Excel 的表达式和自动填充功能了,那么上手计算器上的数据表格功能对你来说也不应当有太大的困难。我们按下 … 工具键(就在那个小长条的下面)。按动上下键选择 公式填充,按下 OK 或 EXE 进入公式填充编辑界面。

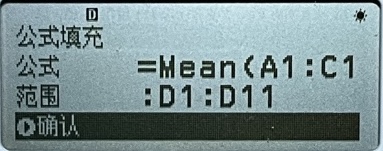


现在,高亮在 公式 = 上。我们按动 OK 或 EXE 键,现在在 公式 = 后面的空白处输入我们的公式 Mean(A1:C1)/50。你或许要问,这个 Mean() 函数、A1:C1 是什么鬼?相信你的 Excel 经验和数学知识,Mean() 函数就是求平均值的函数,A1:C1 是指从 A1 到 C1 的数据范围。那么如何键入呢?我们按动 📖 目录键,选择 数据表格 >。此时你已经可以看到 数据抓取、=、$、:,按动 ⏬️ 往下翻一页就可以看到 均值 了。按下 OK 或 EXE 选中该项,屏幕上就会显示出 公式 = Mean( 的文字。
接下来我们来输入单元格:实际上有两种方法。第一种方法 是使用刚才看到的 数据抓取 功能,按下 OK 或 EXE,然后移动光标到 A1,按下 EXE,再在刚才的地方选择 :,再抓取 C1,最后补全括号,按下 除号 和 50,按下 EXE 确认。第二种方法 是直接通过键盘输入。我们在 = Mean( 后的光标处按下 SHIFT 键,找到黄色字母 A 对应的按键 4,按下 4,光标处就会显示出 A。然后按下 1,再在刚才的地方找到 :,选择它,然后用同样的方法输入 C1,最后补全括号,按下 除号 和 50,按下 EXE 确认。

对于 范围 : 部分,打开该界面的时候已经默认填入了当前单元格 D1:D1,我们只需要移动光标到第二个 D1 后面,把 D 行数 1 改成 11,按下 EXE 确认就可以了。然后按下 OK 或 EXE,我们就完成了公式填充。此时,数据表格中的 D 列就显示出了测量数据的 $\bar{T}$。对于 E 列,我们如法炮制,在 E1 处选择 公式填充,输入公式 D1,按下平方功能键,然后设置填充范围 E1:E11,就得到了 $T^2$ 的数据。

现在我们已经得到了 $\bar{T}$ 和 $T^2$ 的数据。把它们记录到实验报告上,我们还需要对 $m$ 和 $T^2$ 的关系进行线性回归。这个时候,我们可以利用计算器的统计功能来完成这个工作。
利用统计功能进行线性回归计算
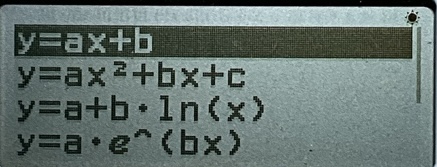
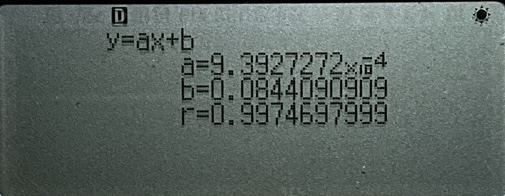
还是按下 主屏幕 键,选择 统计 功能,按下 OK 或 EXE 进入统计功能界面。我们选择 双变量统计,确认。像刚才在数据表格中一样,我们分别把 $m$ 和 $T^2$ 的数据输入到 X 和 Y 列中。然后按下 OK 或 EXE,选择 回归计算结果,再选择 y=ax+b(这里还有很多种函数类型可以在其他的模型中做拟合),按下 OK 或 EXE,就可以看到线性回归的结果了。




总结
今天我们学习了如何使用卡西欧 fx-999CN CW 的数据表格功能和统计功能来加速处理大物实验数据。希望你也能善用计算器,提高实验效率。如果你有更多的问题,欢迎在评论区留言或者发邮件给我,我会尽力解答。

