在工程领域,我们经常会遇到一些非线性方程,比如简谐振动的位移方程、阻尼振动的速度方程等。这些方程通常难以直接求解,但是我们可以借助计算器来进行数值计算。今天我继续来分享如何使用卡西欧 fx-999CN CW 计算器来求解非线性方程。
要求解的问题 一个质量为 m m m d d d k k k x x x t t t x ( t ) = A cos ( ω t + φ ) x(t) = A \cos(\omega t + \varphi) x ( t ) = A cos ( ω t + φ ) A A A ω \omega ω φ \varphi φ t = 0 t = 0 t = 0 O O O P P P v 0 v_0 v 0 θ \theta θ t 1 t_1 t 1
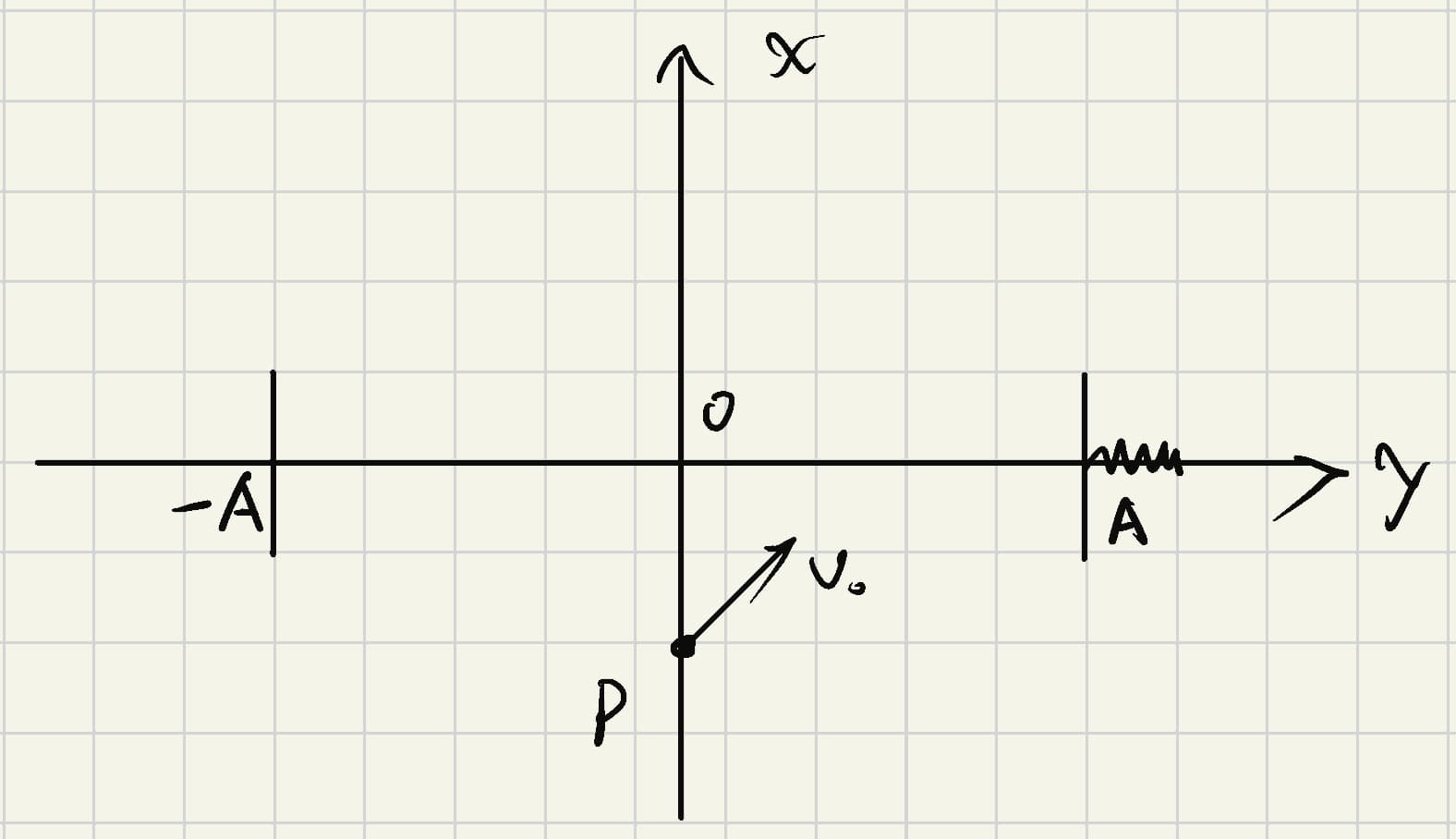
已知 d = 0.2 m d = 0.2\ \text{m} d = 0.2 m m = 0.5 kg m = 0.5\ \text{kg} m = 0.5 kg k = 10 N/m k = 10\ \text{N/m} k = 10 N/m A = 0.45 m A = 0.45\ \text{m} A = 0.45 m O P = 0.2 m OP = 0.2\ \text{m} OP = 0.2 m v 0 = 2 m/s v_0 = 2\ \text{m/s} v 0 = 2 m/s θ = 45 ∘ \theta = 45^\circ θ = 4 5 ∘ g = 9.8 m/s 2 g = 9.8\ \text{m/s}^2 g = 9.8 m/s 2
利用计算器求解 分析平板的运动 平板受到弹簧的约束,所以平板的运动方程是一个简谐振动方程。我们可以通过简谐振动的位移方程来求解平板的位移 x ( t ) x(t) x ( t ) t t t
φ = 0 , ω = k m . \varphi = 0,\quad \omega = \sqrt{\frac{k}{m}}. φ = 0 , ω = m k .
使用计算器代入数据,在 计算 模式下输入 10 0.5 \sqrt{\frac{10}{0.5}} 0.5 10 EXE,得到 ω = 2 5 rad/s \omega = 2\sqrt 5\ \text{rad/s} ω = 2 5 rad/s x 1 ( t ) = 0.45 cos ( 2 5 t ) x_1(t) = 0.45\cos(2\sqrt 5 t) x 1 ( t ) = 0.45 cos ( 2 5 t )
分析小球的运动 将小球的斜抛运动分解为竖直方向和水平方向的运动。竖直方向仅受重力,做匀变速运动;水平方向则是匀速运动。即
y 2 ( t ) = v 0 t cos θ − 1 2 g t 2 + y P , x 2 ( t ) = v 0 t cos θ . y_2(t) = v_0 t \cos\theta - \frac 1 2 g t^2 + y_P, \quad x_2(t) = v_0 t \cos\theta. y 2 ( t ) = v 0 t cos θ − 2 1 g t 2 + y P , x 2 ( t ) = v 0 t cos θ .
代入数据,得到
y 2 ( t ) = 2 t − 4.9 t 2 − 0.2 , x 2 ( t ) = 2 t . y_2(t) = \sqrt 2 t - 4.9 t^2 - 0.2, \quad x_2(t) = \sqrt 2 t. y 2 ( t ) = 2 t − 4.9 t 2 − 0.2 , x 2 ( t ) = 2 t .
求解碰撞时间 小球要与平板能够碰撞,必须满足 − d 2 ≤ y 2 ( t 1 ) ≤ d 2 - \frac d 2 \leq y_2(t_1) \leq \frac d 2 − 2 d ≤ y 2 ( t 1 ) ≤ 2 d x 2 ( t 1 ) = x 1 ( t 1 ) x_2(t_1) = x_1(t_1) x 2 ( t 1 ) = x 1 ( t 1 ) t 1 t_1 t 1 t 1 t_1 t 1
首先,我们利用第一个方程来解出 t 1 t_1 t 1
− 0.1 ≤ 2 t 1 − 4.9 t 1 2 − 0.2 ≤ 0.1 -0.1 \leq \sqrt 2 t_1 - 4.9 t_1^2 - 0.2 \leq 0.1 − 0.1 ≤ 2 t 1 − 4.9 t 1 2 − 0.2 ≤ 0.1
实际上就是求解方程 2 t 1 − 4.9 t 1 2 − 0.2 = − 0.1 \sqrt 2 t_1 - 4.9 t_1^2 - 0.2 = -0.1 2 t 1 − 4.9 t 1 2 − 0.2 = − 0.1 主屏幕 键,移动高亮到 方程,按下 OK,选择 多项式方程,再选择 ax^2 + bx +c。移动光标键入系数 -4.9、√(2)、-0.2--0.1。
5 2 − 1 49 ≤ t 1 ≤ 5 2 + 1 49 , \frac{5\sqrt 2 - 1}{49} \leq t_1 \leq \frac{5\sqrt 2 + 1}{49}, 49 5 2 − 1 ≤ t 1 ≤ 49 5 2 + 1 ,
0.12 ≤ t 1 ≤ 0.17. 0.12 \leq t_1 \leq 0.17. 0.12 ≤ t 1 ≤ 0.17.
然后,我们利用第二个方程来求解 t 1 t_1 t 1
2 t 1 = 0.45 cos ( 2 5 t 1 ) \sqrt 2 t_1 = 0.45\cos(2\sqrt 5 t_1) 2 t 1 = 0.45 cos ( 2 5 t 1 )
这是一个非线性方程,我们可以通过计算器来求解。按下 主屏幕 键,移动高亮到 方程,按下 OK,选择 求解方程,输入 2 x = 0.45 cos ( 2 5 x ) \sqrt 2 x = 0.45\cos(2\sqrt 5 x) 2 x = 0.45 cos ( 2 5 x ) EXE,设定迭代初始值为 0.12 0.12 0.12 t 1 t_1 t 1
t 1 ≈ 0.318 s . t_1 \approx 0.318 \ \text{s}. t 1 ≈ 0.318 s .
由于 t 1 t_1 t 1 t 1 ≈ 0.318 s t_1 \approx 0.318 \text{s} t 1 ≈ 0.318 s
总结 今天我们利用计算器解决了一个涉及到简谐振动和斜抛运动的问题。通过计算器的方程求解功能,我们可以快速地求解非线性方程,帮助我们更好地理解问题。希望这篇文章对你有所帮助!
 解得范围为
解得范围为
 大约是
大约是

